 ラジグラ
ラジグラさて、エンコーディングをやりますか!?



え!?横文字理解できませんので優しく!
言葉の理解からしていく!エンコーディング
結構、言葉の意味って重要です!エンコーディングとは?っていきなり聞かれるとなんとなくのイメージはあるけど、正味わからんって場合がありますよね!
つまり、今回のテーマであるスライス選択はスライスエンコーディングのことになり、スライス方向に符号をつけるということになります。なんで符号化しないといけないの?ということですが、触りは以下の記事でやりました。復習ついでにやっていこうと思います。


スライス選択とはなにか?
以前の記事でもやりましたが、静磁場の中に人体が入った場合、人体の水素原子は歳差運動の速度(周波数)はすべて一緒になってしまいます。
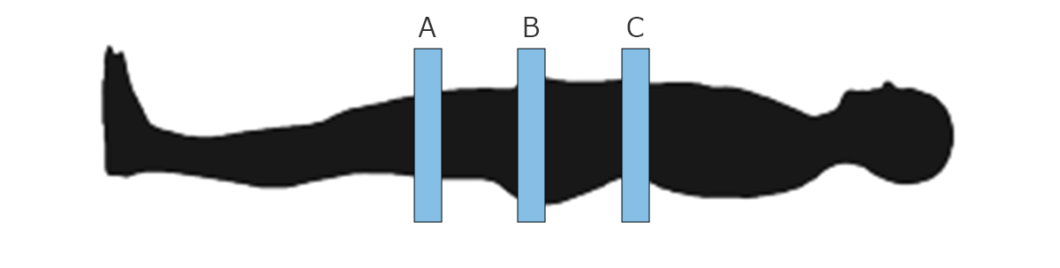

何を言いたいかというと上の図でA・B・Cとスライスがある場合、スライスの中のラーモア周波数はすべて同じになっているために位置を同定できません。ここで先程のスライス選択(スライスエンコーディング)をしてそれぞれを符号化することで同定をします。
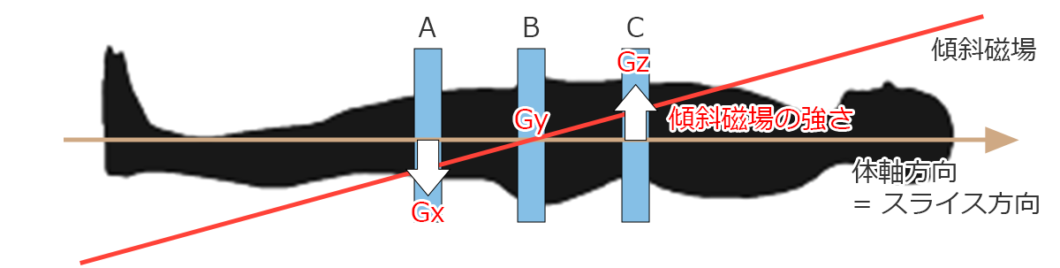

スライス方向の傾斜磁場を印加することでラーモア周波数の計算式よりそれぞれの位置の周波数を変えることができ、これがエンコーディング(符号化)ということになります。
Aの位置:ωx =γ ×(B0 + Gx × X)
Bの位置:ωy =γ ×(B0 + Gy × X)
Cの位置:ωz =γ ×(B0 + Gz × X)
スライス選択を深堀りしていく
ざっくりの概要はわかったと思います。もう少し深堀りをするために1スライス(今回はAとします)を分解していきますね。
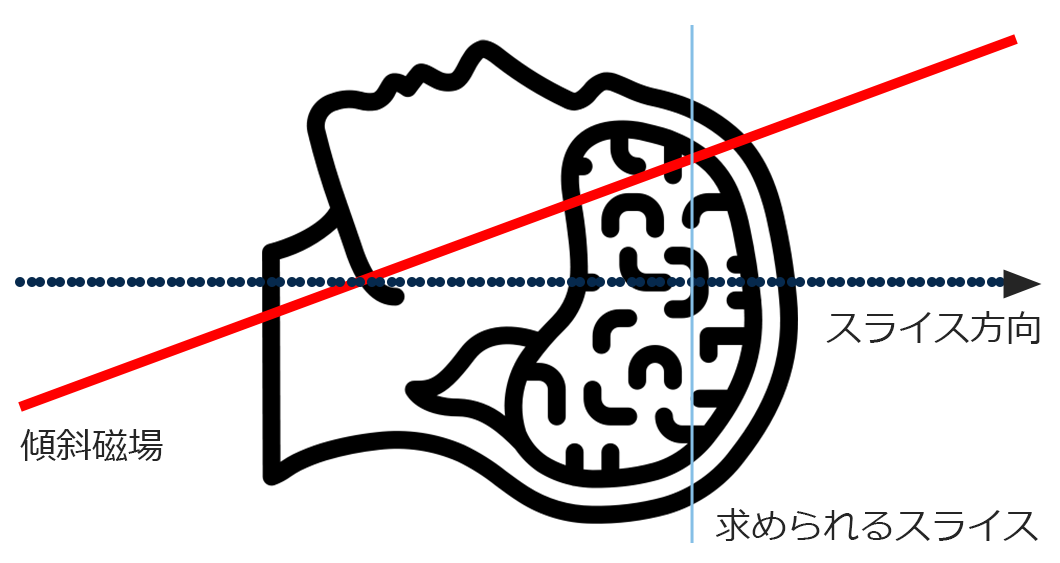

上の図のようにスライス方向の傾斜磁場を印加して、特定の周波数(上の計算式で求めたAの位置 ωx =γ ×(B0 + Gx × X)を使います)で同定させた場合、上の図のように線上の情報(青線)しか収集することができません。理由はラーモアの周波数がωxと単一周波数だからです。単一周波数だとスライスが何枚あれば全脳撮影ができるか…気が遠くなりますね!なので私達の検査で下のは常にスライス厚を設定して検査をしております。
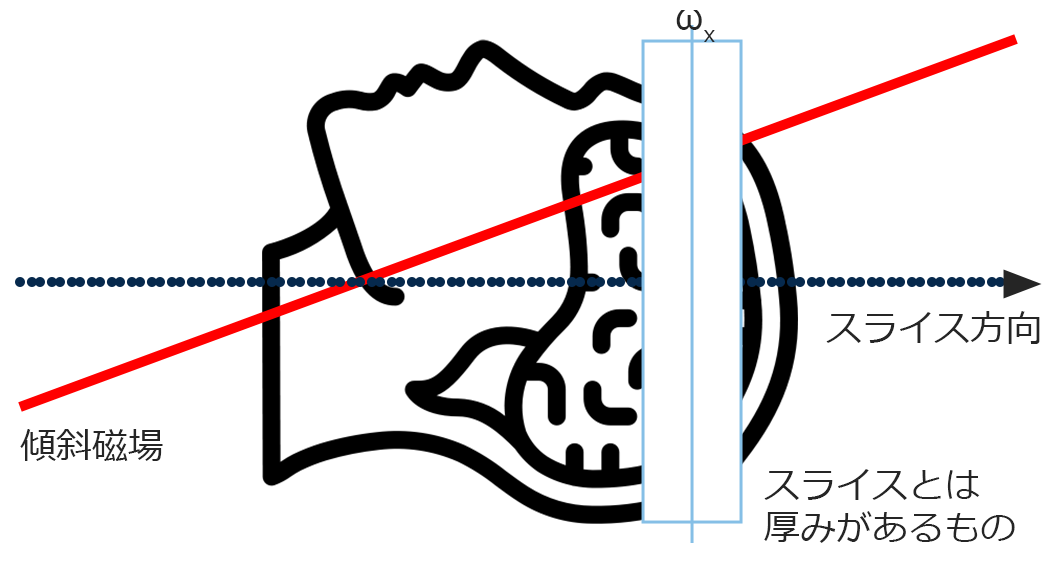

前述しましたが、上の図のようにでωxに厚みを持たせないと到底検査を終わらせることはできません。この厚みをもたせる方法は下の図のように今回の周波数ωXに周波数幅を±⊿ωを持たせることで解決することができます。
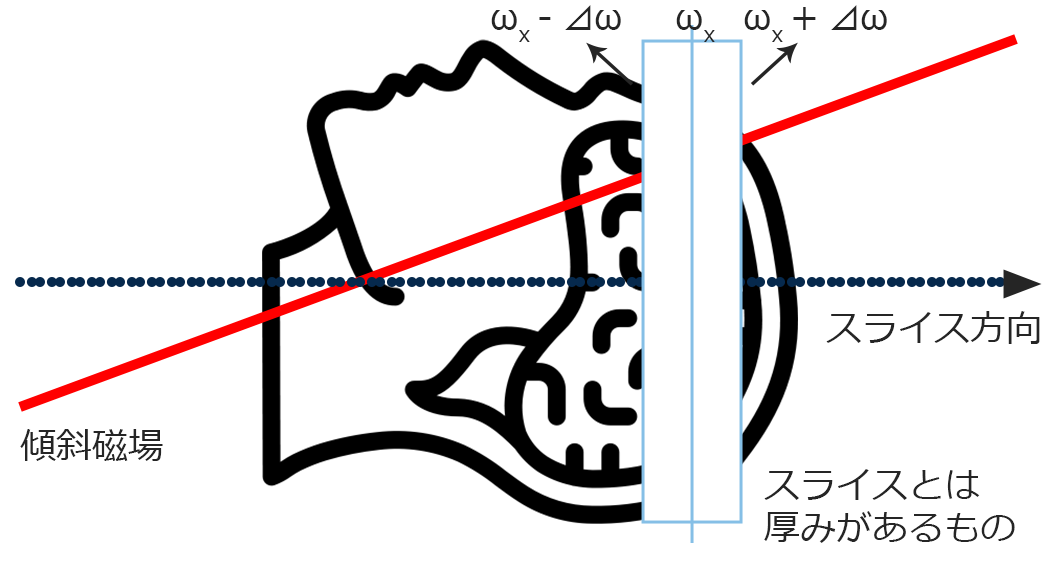

共鳴させる周波数とスライス厚の関係がわかると思います。この周波数幅を送信バンド幅といいます。また、この⊿ωを大きくすればスライス厚も太くなり、⊿ωを小さくすればスライス厚も薄くなります。
スライス厚を可変するには?
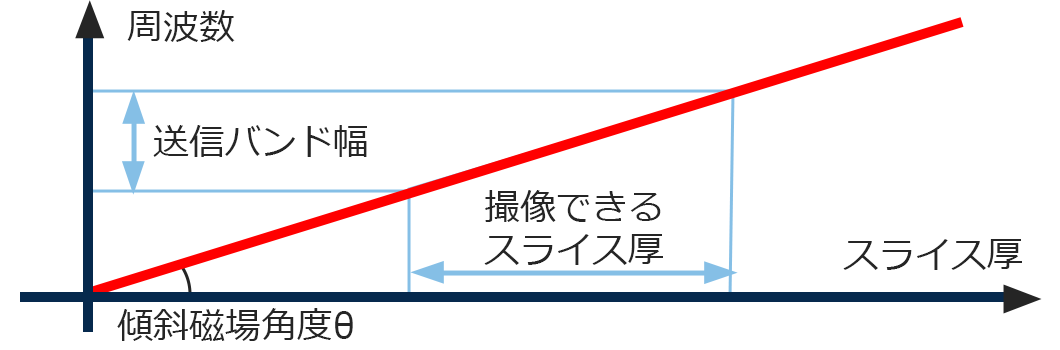

さて、さきほどは頭で説明をしました。今度はグラフです。横軸にスライス厚、縦軸に周波数のグラフになります。グラフの角度は傾斜磁場角度θとします。ここに送信バンド幅と撮像できるスライス厚の注釈をいれました。
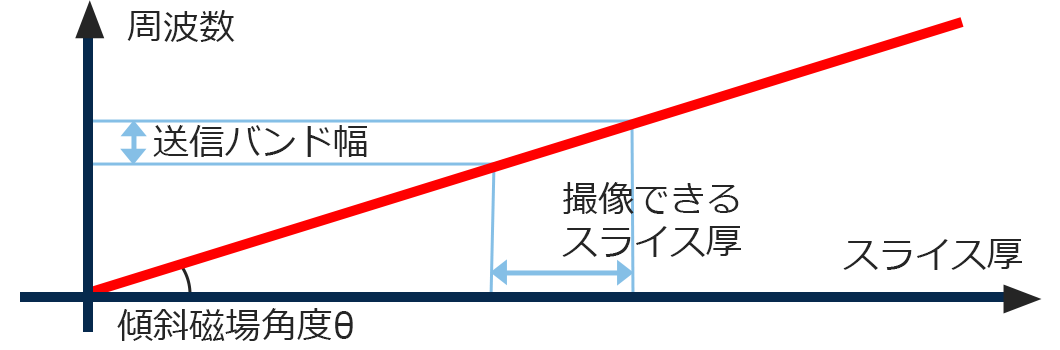

スライス厚を可変させる方法は先程も述べましたが、送信バンド幅(特に⊿ω)を動かすことでスライス厚を変えることができます。しかし、送信バンド幅にも限界がありますのでもう一つの方法があります。
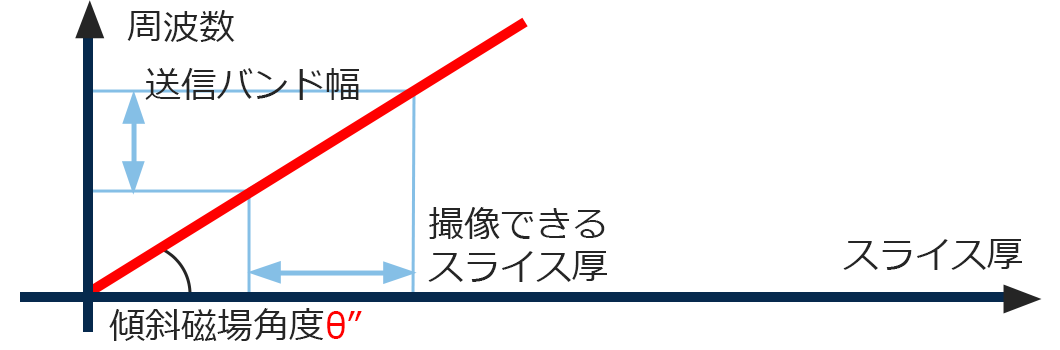

今度は磁場角度をθからθ”に変えました。こうすることで送信バンド幅を変えずに(二個上の画像と比較してみてください)撮像できるスライス厚を薄くすることができます。送信バンド幅の限界にふれることなくスライス厚を調整できます。また、言い換えると傾斜磁場が強くかけられる装置は薄いスライスを撮像できるということになります。MRI装置の購入時などにこういう基礎が役にたちます。
エンコードについて(スライス選択)のまとめ
さて、スライス選択は理解に苦しむのはあまりないと思います。そこまで難しくないと思います。そして、これをしっかり理解することで、位相エンコードや周波数エンコードが理解できるようになりますのでしっかり押さえておきましょう!
- 傾斜磁場を印加して周波数の違いをだしている
- 周波数に幅をもたせることでスライス厚の概念に合わせている
- 周波数に幅をもたせてことを送信バンド幅という
- 送信バンド幅とスライス厚は相関関係にある
- スライス厚を変更するには送信バンド幅を可変させる
- スライス厚を可変するには傾斜磁場を強くしたり、弱くしたりしている



