 ラジグラ
ラジグラこれ一番説明が難しいのよね…



今までも十分にむずかしいわ!PSD
面内の位置決めをするために周波数と位相を使う!
前回の記事でスライス選択についてやりました。要約すると共鳴する周波数を傾斜磁場を使って振り分けを行い、スライス位置を同定する方法でしたね!今回は、面内のお話になります。傾斜磁場を使って、周波数だけでは面内の水素原子は同定できません。さて、毎回ですが言葉の意味からやってやっていきます。
- 周波数エンコード
-
周波数を使って、X軸方向のエンコード(符号化)させる方法
- 位相エンコード
-
位相差を使って、Y軸方向のエンコード(符号化)させる方法
違いは言葉からわかるように「周波数」と「位相」ですね!なんで「周波数」と「位相」なのかは後述します。この2つをわかりやすく図にしてみました。
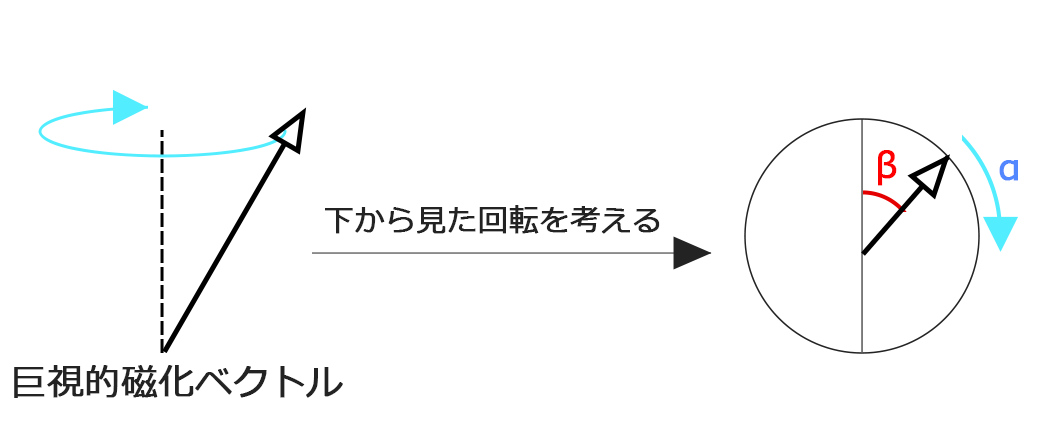

巨視的磁化のことを磁化やスピンともいいます。この方向(今回の図では上方向)を軸とする歳差運動をしています。これがラーモア(Larmor)の歳差運動といい、記事の途中で出した数式(ω = γ × B0)で回転の周波数を出すことができます。そして、この巨視的磁化ベクトルを下から見て、スタートポイントであるβを位相とし、回転スピードであるαを周波数といいます。
周波数と位相を切り分けて考える
今回、PSD(Pulse sequence diagram)の説明でずっとSE法(Spin Ech法)で進んでいますので、今回も周波数変換と位相変換部分を切り取ってみました。
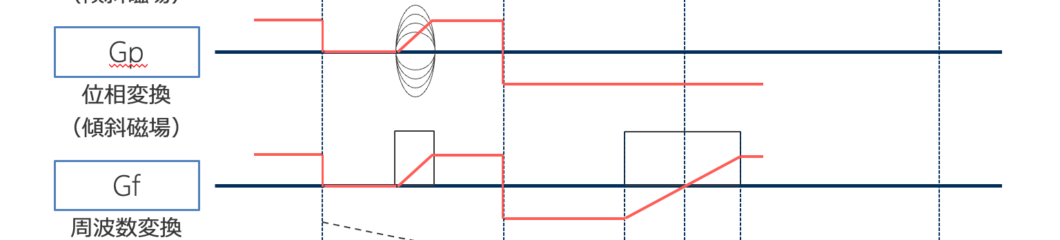

今回のテーマはエンコーディングなので、以下の部分(青四角部分)の説明になります。
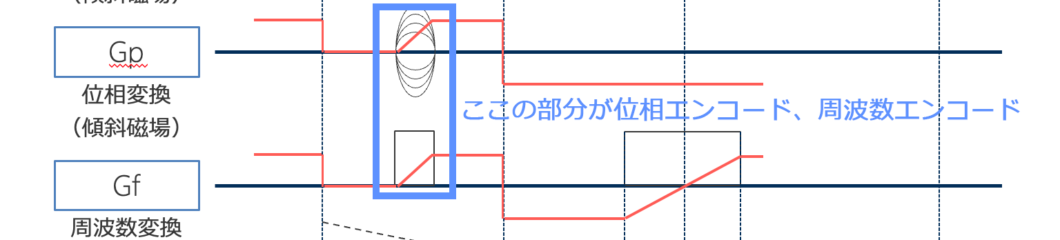

そして、ダンゴムシの部分を説明しやすいように決めます。今回は周波数マトリクスと位相マトリクスを「3」とします。
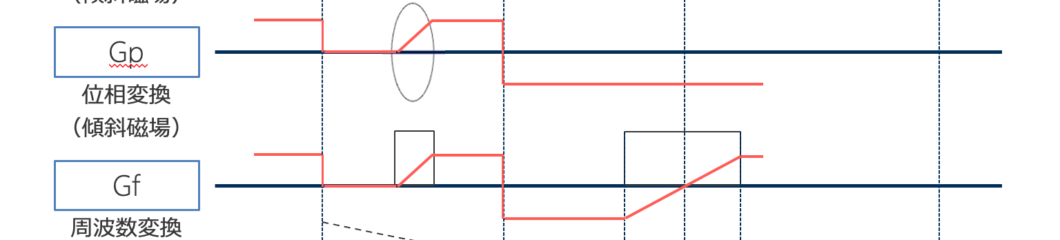

徹底分解!周波数エンコードと位相エンコード
流れは作れたのでここから徹底的に分解してやっていきます。まず、1回目のTR内で起きることをやります。下の図では3×3マトリクス内の巨視的磁化ベクトルを表示しています。左側がなにも印加していない状況です。そして、周波数方向の傾斜磁場を印加したのが右側です。
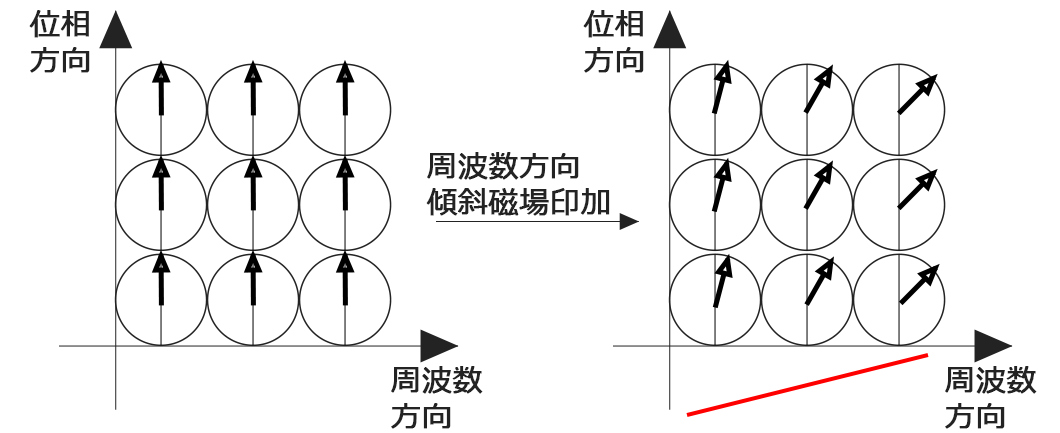

周波数方向に傾斜磁場を印加したことで3×3のマトリクス内は3種類に分けることができました。周波数を動かしたので回転スピードがそれぞれ変わりました。ここで注目してほしいのが一番右端を例にすると上・中・下で矢印の向きの差がないことです。つまり、この3マトリクスは分解できないことがわかると思います。ここでデータ収集しても縦方向の分離ができないので画像化することができないということになります。
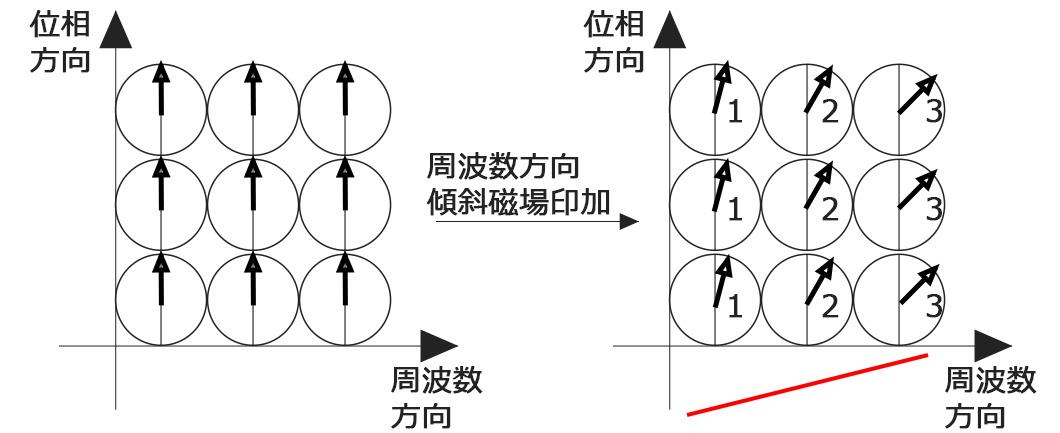

説明が難しいので周波数を簡易的に数値化してみました。なにが言いたかったかというと周波数が「3」が3つもあるので差がわからないということですね。今後は3つある数字を差別化しないといけません。同じように周波数傾斜磁場を縦軸にすればいいと思う方もいらっしゃると思うのでやってみましょう。
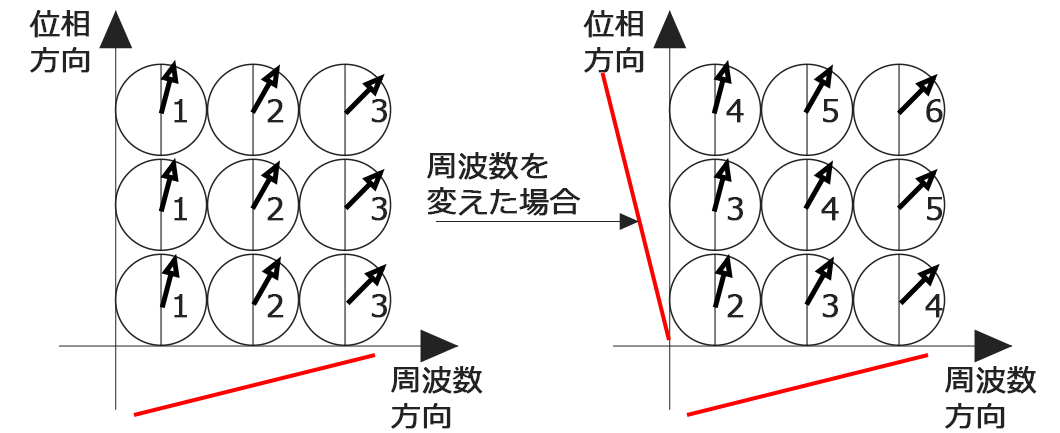

周波数を縦軸に対しても変えてみました。法則はさきほどと同じです。さきほどは「1・2・3」が切り分けできなかったのですが、周波数のみでやっても今度は「3・4・5」が切り分けできなくなります。このような事態になるので上で説明したスタートポイントであるβ=位相を使います。
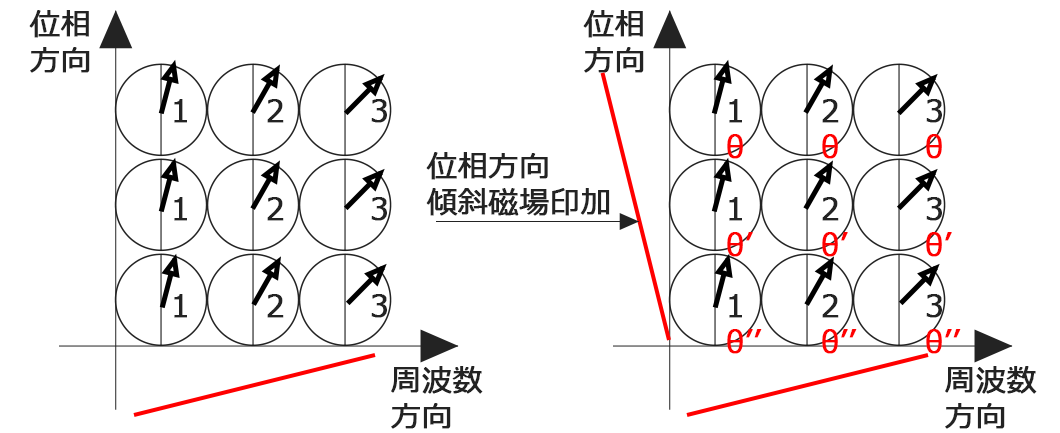

位相情報を「θ」としました。すると情報が2つ(周波数と位相)になったことで各マトリクスの情報が全部分離できたのがわかると思います。すばらしい!考えた人すごいなーと思います。そして、これでやっと1回目のTRが終わります。
少しむずかしい話をします。今巨視的磁化ベクトルを数値として表示はしているのですが、実際は波を収集しますので数値以上に難しく、単純に求められるものではありません。しかし、波なので波の周期における位置と角度という情報があり、そこから算出をしています。その際に使われる式が以下の通りになります。
ωが周波数、θが位相になります。上ではα(周波数)、β(位相)として表現しています。この式があるので周波数と位相を使ったというのが最大の理由になります。
位相情報を繰り返して付与する
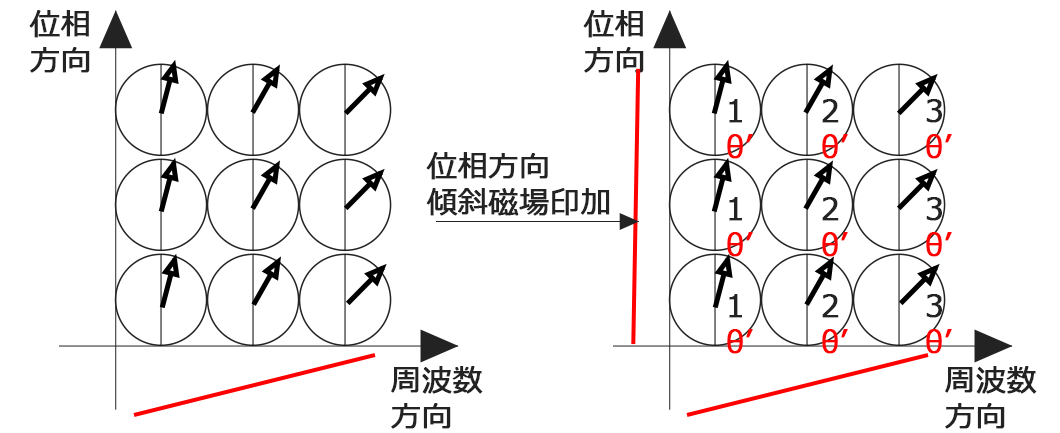
さて、今説明した図をみると全部のマトリクスが分離できたので1回のTRで終了でいいよね?ってなりますが実際は違います。説明をしていくと難しい方向に進んでしまうので割愛します。さて、2回目のTRをやっていきましょう。今度は位相傾斜磁場を印加しないターンですね!

で、3回目のTRでの位相傾斜磁場を印加した場合もやります。
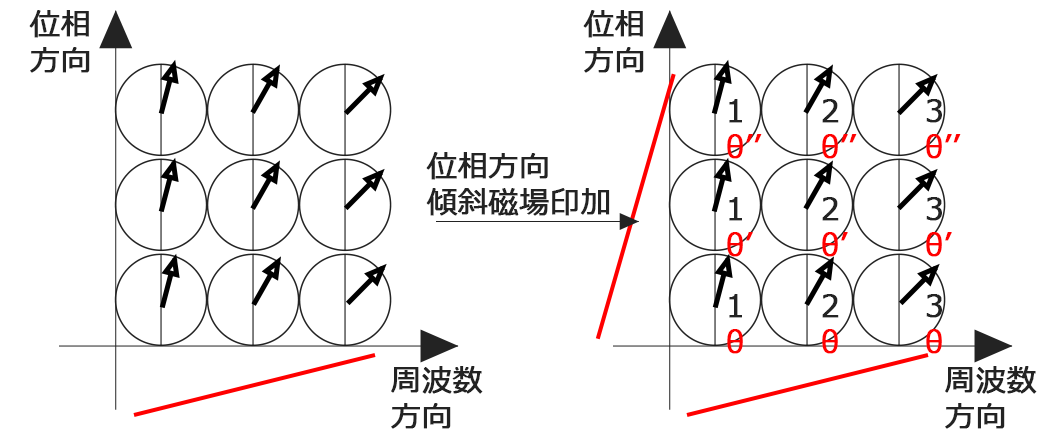

PSDからわかるように位相方向の傾斜磁場印加は1回目の逆になりますので、位相情報は逆になるといった感じです。一旦まとめてみましょう。
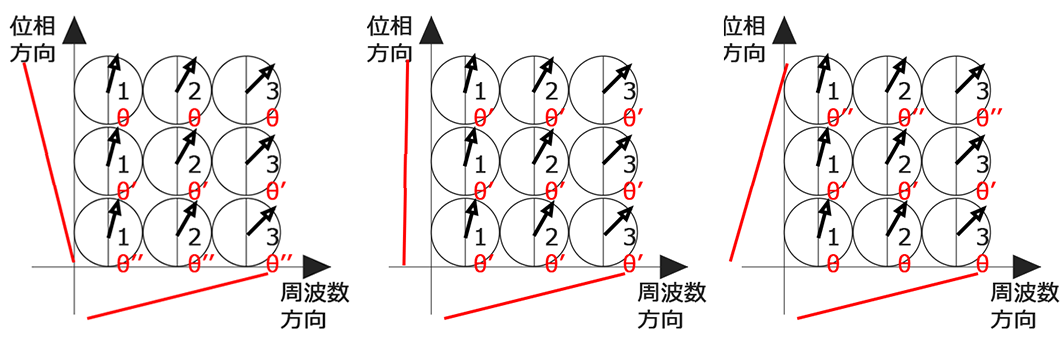

まとめをみるとわかるように全部で27マトリクス分(TR3回×9マス)の情報がk空間に入れられて画像化されていきます。いや、本当に難しくて合成波などの話はすべて闇に放り込みました!これは今度!
周波数エンコードと位相エンコードのまとめ
合成波などの説明をぬいたおかげでなんとなくk空間に詰めるデータについてわかったと思います。切り抜いて切り抜いて丁寧に考えるしかないんですよね。エンコード=符号化している中身が少しでも伝われば!
- 巨視的磁化ベクトルを分解して、位相(β)と周波数(α)を表した
- sin(ωt + θ)の数式から周波数(ω)と位相(θ)の情報で波を観測して分解できる
- TR毎にデータを収集して、k空間に詰め込んでいる
- 収集したデータを簡易的に数値化して説明をした



