 ラジグラ
ラジグラついに難題のk-space(k空間)へいくか



(沈黙…)
そもそもk-space(k空間)とはなにか?
k-space(k空間)はごちゃこちゃなイメージでなかなか実態を理解するのが難しくて、自分も結構敬遠したくなる内容です。少し大変ではありますがやってみます。混乱させたら、本当にごめんなさい!
そもそもk-space(k空間)とは、空間周波数領域であることが定義とされています。ドイツの物理学者:kayserが以下の式を定義付けしました。
k = γ × G × T
γ:磁気回転比(Hz/T)
G:傾斜磁場強度(T/m)
T:印加時間(s)
そして、MRIの実空間は位置座標(位相方向と周波数方向)で表すことができますが、k-space(k空間)では空間周波数を座標としています。
空間周波数とは?

上にk-space(k空間)のイメージ図を出しました。四角形にすると画像の枠のように思えますが、横軸がxで縦軸がyの単なるグラフでしかないんですね。
空間周波数は周波数とは違います。これが混乱の原因なんですよね。想像しにくいという…
空間周波数とは「空間的に明暗が変動するような縞模様の波動に対して使われる周波数」となります。この説明ではよくわかりにくいですが、縞々の波を数値化したものと思ってください。参考イメージ図を載せておきますが、この縞々を数値にしたものが空間周波数ということになります。


さて、上の計算式では空間周波数(縞々を数値化した)というのがわかりにくいので、まずは普通に単位のみで計算してみましょう。
k = γ × G × T = (Hz/T) × (T/m))× (s)= (Hz) × (1/m) × (s)
混乱してきますね!Hzは1/sと書き換えることができますので式は以下のように変化します。
k = γ × G × T = (Hz/T) × (T/m))× (s)= (Hz) × (1/m) × (s)=(1/s)×(1/m)×(s)=(1/m)
単位は毎メートルになりました。訳すとkには1メートルあたりにに1周期があるというデータになりました。そして、周期とはさきほど説明した縞々模様の周期になります。なんとなくわかるようなわからないようなですよね。
今度は周波数を同義である振動数(cycle/m)に変換して単位の計算をしてみます。
k = γ × G × T = (Hz/T) × (T/m))× (s)= (cycle/m/T) × (T/m) × (s) = (cycle/s)
ある単位(今回はs:秒)でなんかのサイクルに変換できました。このなんかのサイクルというのは前述した縞々の波(サイクル)ということになります。この2つの単位からkは縞々の周期・サイクルを表していることが伝わってくれれば嬉しいです。kを10と仮定すると10cycle/sなので1秒間に10サイクルの縞々模様だということになります。
実際、kはどうやって求められる?


再掲にはなりますが、このkという縞々サイクルを表した数値はどこですか?というのがk空間(グラフ)なのです。y方向(縦方向)の縞々が多ければ上もしくは下、少なければ縦方向の中央ということ、x方向の縞々が多ければ右もしくは左、少なければ横方向の中央ということになります。わかりやすくするためにk-space(k空間)を下の図のようにグラフにしちゃいましょう。
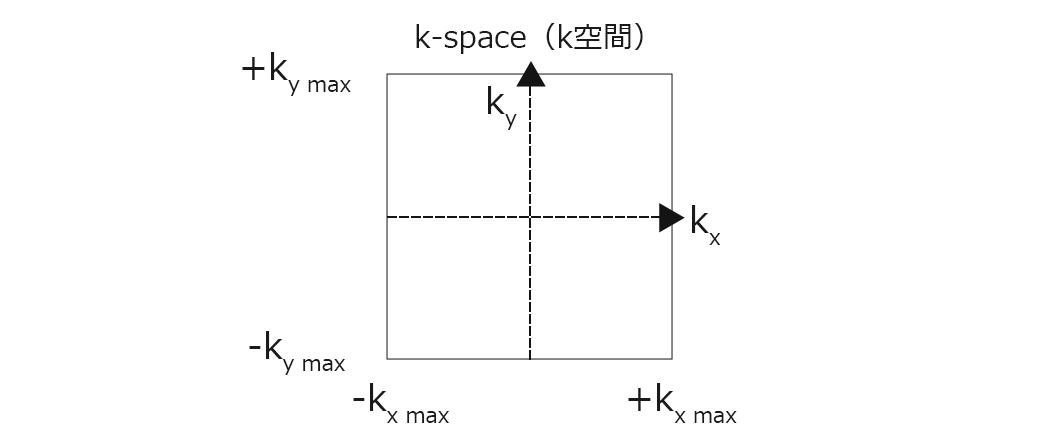

kというデータをどこに置くかというグラフであるk-space(k空間)というのがわかりました。では、置く場所をどうやって決めているかというのも式からもう一度考えてみましょう。
k = γ × G × T
γ:磁気回転比(Hz/T)
G:傾斜磁場強度(T/m)
T:印加時間(s)
まず、簡単に思いつくのがGとTですね。これをコントロールしているのが傾斜磁場になります。傾斜磁場についてはこの記事でこの話を少ししました。


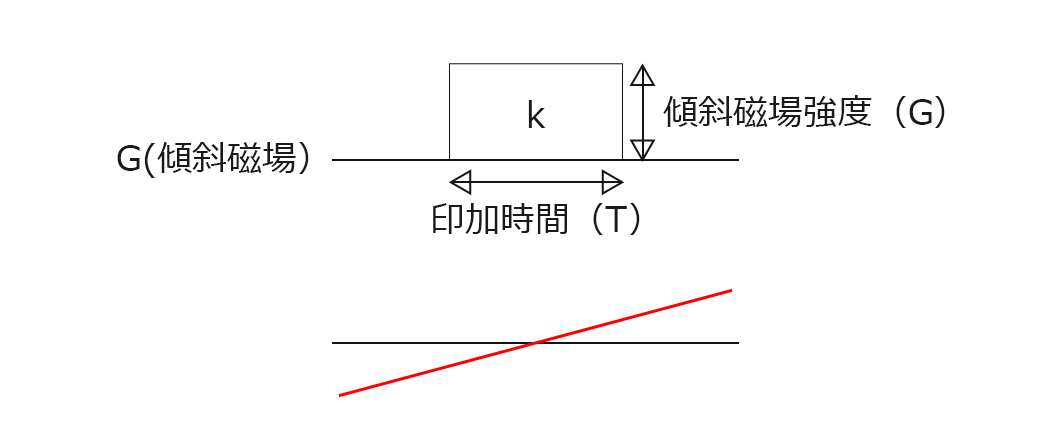

kの式からわかるようにGとTを乗じているので上の図の傾斜磁場面積が求められます。この傾斜磁場面積はkと相関があることが式から推察できます。ここの段階で式からγ(磁気回転比)がわかりませんが、傾斜磁場を印加していることからラーモア周波数の式から割り出すことができます。ラーモア周波数の式についてはこの記事に書きました。


ラーモア周波数 ω = γ × B0
ω:歳差運動周波数
γ:磁気回転比 42.6MHz/T(水素原子核)
B0:静磁場強度
少しまとめます。
あとは求められたk(つまり縞々模様のデータ)を置くことでk-space(k空間)が完成します。
k-space(k空間)を覗いてみるのまとめ
k-spaceがなにかというのが少しでも伝わればいいとは思いますが、逆に混乱をさせてしまった場合は本当にごめんなさい。最後にまとめていきます。
- k-spaceでは空間周波数を使っている
- k = γ × G × T と定義されている
- 定義されている式は縞々のサイクルを表している
- 求められたkをグラフに配置して出来上がったのがk-space(k空間)である
- kは傾斜磁場を印加することで数式の数値を決めることができる
- ここでもラーモア周波数が助けとなる



